skip to content

Understanding & modifying vertex positions in ThreeJS

Tags: #threejs #webgl
Last updated: Jul 2, 2023

I've been on-and-off, slowwwwly, learning more about ThreeJS and 3D graphics creations. This note originated with me wanting to grab all the corners of a shape like a cube, and add randomness to them to create a fun/funky shape. I ended up digging into how geometries are constructed in ThreeJS and how to create and manipulate the vertices of a particular shape.

Every geometry in ThreeJS is made up of a bunch of segments. Segments are basically lines that divide each face of the shape into triangles.

Segments are set when creating a geometry, like so...

const r = 5
const widthSegments = 1
const heightSegments = 1
const depthSegments = 1
const geometry = new THREE.BoxGeometry(r, r, r, widthSegments, heightSegments, depthSegments)

Here is a box geometry created with 2 segments in each direction:

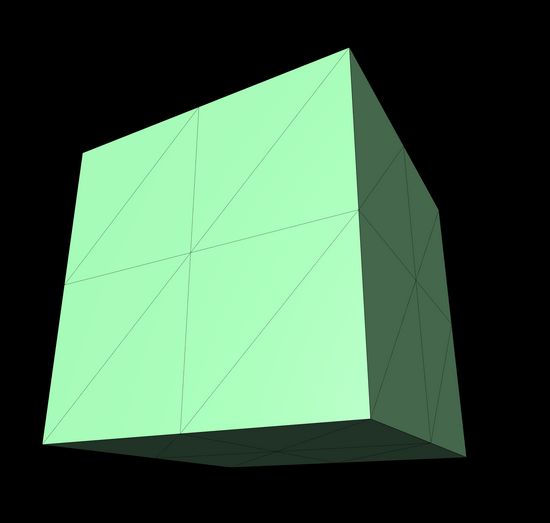
a cube where each face is divided into 4 squares, each with a diagonal line through it

But the default is one per direction, which looks like this:

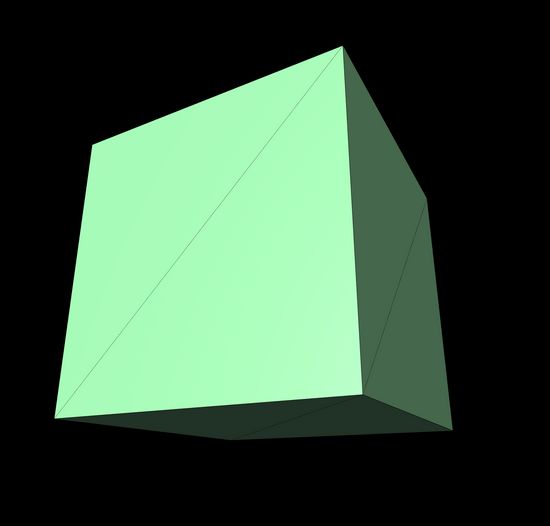
a cube where each face has one diagonal line across it

So let's say we start out with the simplest shape, with one segment in each direction. Each of these geometries has a positions attribute listing all of its vertex positions, which we can get like this:

const positions = geometry.getAttribute('position') as THREE.BufferAttribute
const count = positions.count

If you console.log(positions) here you'll see an object with a few attributes. One is an array with a length of 72. The more important part is actually positions.count which in this case is 24. This means the shape has 24 vertices.

The 24 comes from 1) the shape has 6 faces, and 2) each face has 4 individual points (vertices). I was super confused for a long time because I thought the points were based on how many triangles were in each face, and trying to find some kind of way to multiple 3 points per triangle and 6 faces to get to the right number. But nope.

positions.array has 72 values because each vertex has an x, y, and z value - meaning 24 * 3 = 72 individual values in our array.

If we go back to our shape with 2 segments each way, positions.count is 54. 9 points/vertices on each face, multipled by 6 faces.

We can get a particular point from this positions array and modify it like this:

let n = 0 // position index
let point = new THREE.Vector3()
point = point.fromBufferAttribute(positions, n)

// modify the position
let x = point.x * Math.random()
let y = point.y * Math.random()
let z = point.z * Math.random()
positions.setXYZ(n, x, y, z)

But if we just loop through the points and randomize the values on all of them, it looks like this, which is not what we want:

It's... not really a shape anymore. The problem is that many of the vertices in positions are duplicated. The corners of each face of the shape are also corners of another face. For our shape to stay an intact shape, those vertices need to stay the same as each other.

Instead, we can create a simple map to store each position as we iterate through them. On each vertex, we check - have we seen this position before? If we haven't, great, we create some new randomized values and set the position to those values. But if we have, we remind ourselves of the randomized values we already used, and just update the current vertex to match.

let vary = 1.5 // or whatever
const positions = geometry.getAttribute('position')
const count = positions.count
let verticesMap = {}
let point = new THREE.Vector3()

for (let i = 0; i < count; i++) {
	point = point.fromBufferAttribute(positions, i)
	let key = [point.x, point.y, point.z].join(',')

	if (!verticesMap[key]) {
		verticesMap[key] = {
			x: point.x + Math.random() * vary,
			y: point.y + Math.random() * vary,
			z: point.z + Math.random() * vary,
		}
	}

	let { x, y, z } = verticesMap[key]
	positions.setXYZ(i, x, y, z)
}

geometry.computeVertexNormals() // update colors & shading

It works! Have a funky shape:

Resources

← all notes